楔子
本篇文章来探讨一下整数的加减法是怎么做的,因为整数在底层采用数组进行存储,所以它的加减法就不像浮点数那么简单。
在介绍浮点数的时候说过,对于数值型对象,它的类型一定实现了 tp_as_number 字段,该字段指向了 PyNumberMethods 结构体实例。结构体里面的每个字段都是一个函数指针,对应数值型对象的一个操作。
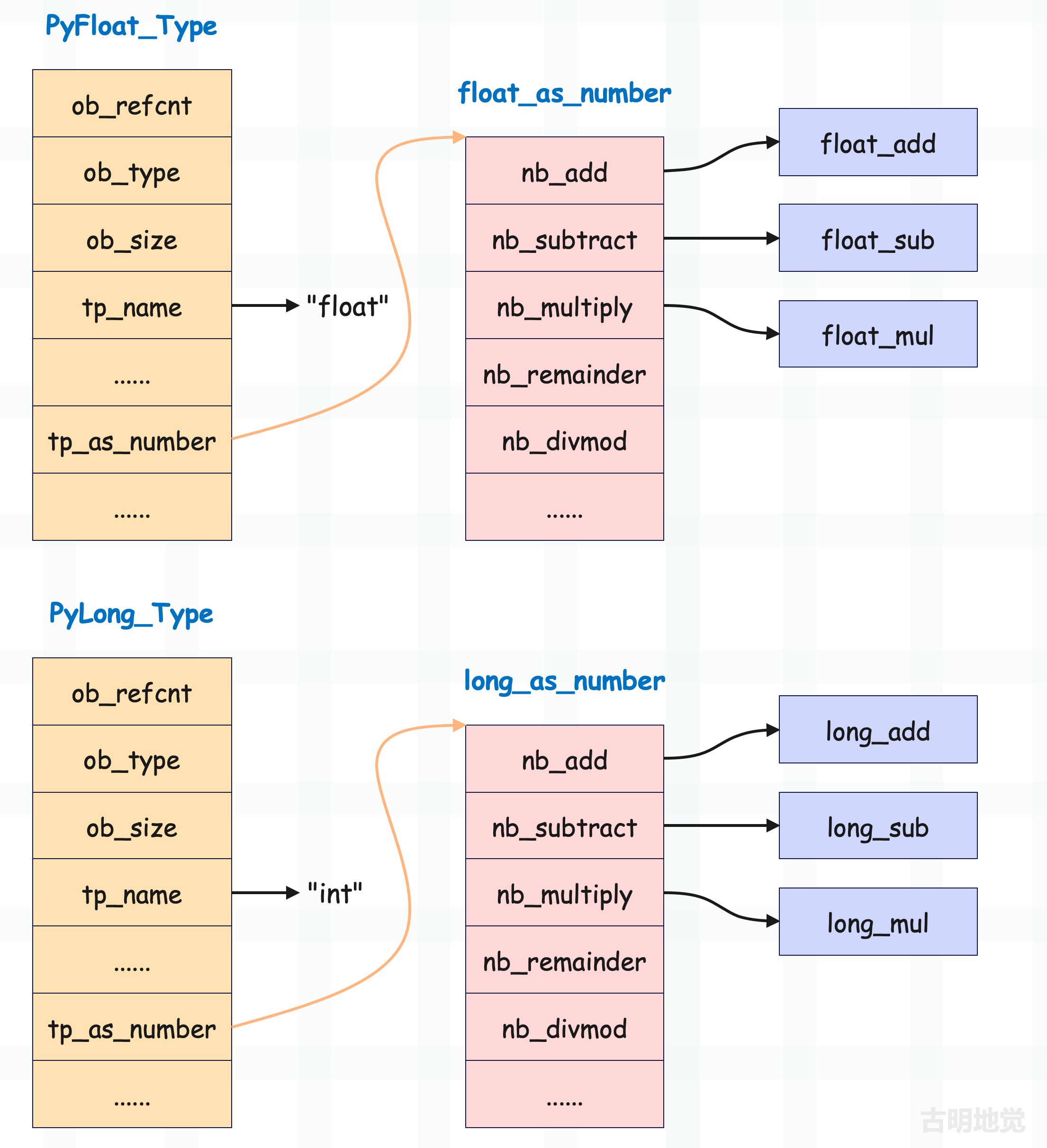
比如 nb_add 负责加法操作,nb_substract 负责减法操作等等,本篇文章就来探讨一下。首先整数支持的操作非常多,这里我们只探讨加减法。
整数加减法的运算原理
整数的加法和减法分别由 long_add 和 long_sub 实现,但运算的核心却不在这两个函数上,它们内部会调用另外两个函数。因为数组保存了整数的绝对值,所以 Python 将整数的运算转成了绝对值运算,而底层有两个函数专门用来做这件事情,分别是 x_add 和 x_sub。
- x_add(a, b):计算 a 和 b 的绝对值之和;
- x_sub(a, b):计算 a 和 b 的绝对值之差;
所以整数相加就可以这么做,假设两个整数 a 和 b 相加:
- 如果 a 和 b 均为正数,那么通过 x_add 计算 a 和 b 的绝对值之和即可;
- 如果 a 和 b 均为负数,那么通过 x_add 计算两者的绝对值之和,然后再取相反数;
- 如果 a 为负数,b 为正数,那么通过 x_sub 计算 b 和 a 的绝对值之差即可;
- 如果 a 为正数,b 为负数,那么通过 x_sub 计算 a 和 b 的绝对值之差即可;
而整数相减也是同理,还是整数 a 和 b,两者相减:
- 如果 a 为正数,b 为负数,那么通过 x_add 计算两者的绝对值之和即可;
- 如果 a 为负数,b 为正数,那么通过 x_add 计算两者的绝对值之和,然后再取相反数;
- 如果 a 和 b 均为正数,那么通过 x_sub 计算 a 和 b 的绝对值之差即可;
- 如果 a 和 b 均为负数,那么通过 x_sub 计算 b 和 a 的绝对值之差即可;
相加时,符号相同会调用 x_add、符号不同会调用 x_sub。相减时,符号相同会调用 x_sub、符号不同会调用 x_add。
所以这就是 Python 的设计,因为绝对值的加减法不用考虑符号的影响,实现更为简单,所以 Python 将整数运算转化成整数的绝对值运算。那么下面我们的重心就在 x_add 和 x_sub 上面了,看看它们是如何对大整数绝对值进行运算的。到这里你可能会有疑问,大整数运算这么复杂,效率会差吧。显然这是啃腚的,整数数值越大,整数对象的底层数组就越长,运算开销也就越大。
但 Python 底层有一个机制叫做快分支,因为通用逻辑能处理所有情况,那么它的效率必然不高。而快分支则是对那些可以简单运算的情况提前进行处理,比如在对 a 和 b 计算加减法的时候,底层会先判断数组的长度是否均小于等于 1,如果是则说明数组中最多只有一个元素。这样的话,就可以直接转成 C 的整数进行运算了,这样性能损耗就可以忽略不计。
关于快分支,需要再单独解释一下。我们举个生活中的例子:好比你去见女朋友,正常情况下,你需要买花,并且精心打扮。但如果女朋友不在生理期,那么这一切都不需要做,只需买杯奶茶就好了。所以先判断女朋友是否在生理期,如果不在,那么只需买杯奶茶就能牵手便属于快分支。快分支具有命中率高等特点,绝大部分都是这个情况,而一旦命中快分支,那么程序便可快速处理。
回到上面的例子,只要整数不超过 2 ** 30 - 1,都可以走快分支,显然这可以满足绝大部分场景,因为这个数字已经很大了。至于 x_add 和 x_sub 则属于通用逻辑,而通用也意味着平庸,但如果快分支没有命中,那么就只能走通用逻辑了。
而我们的重点就是要研究 x_add 和 x_sub 的实现,感受大整数运算的魅力。不过在介绍之前,不妨想象一下我们平时将两个整数相加的时候是怎么做的。
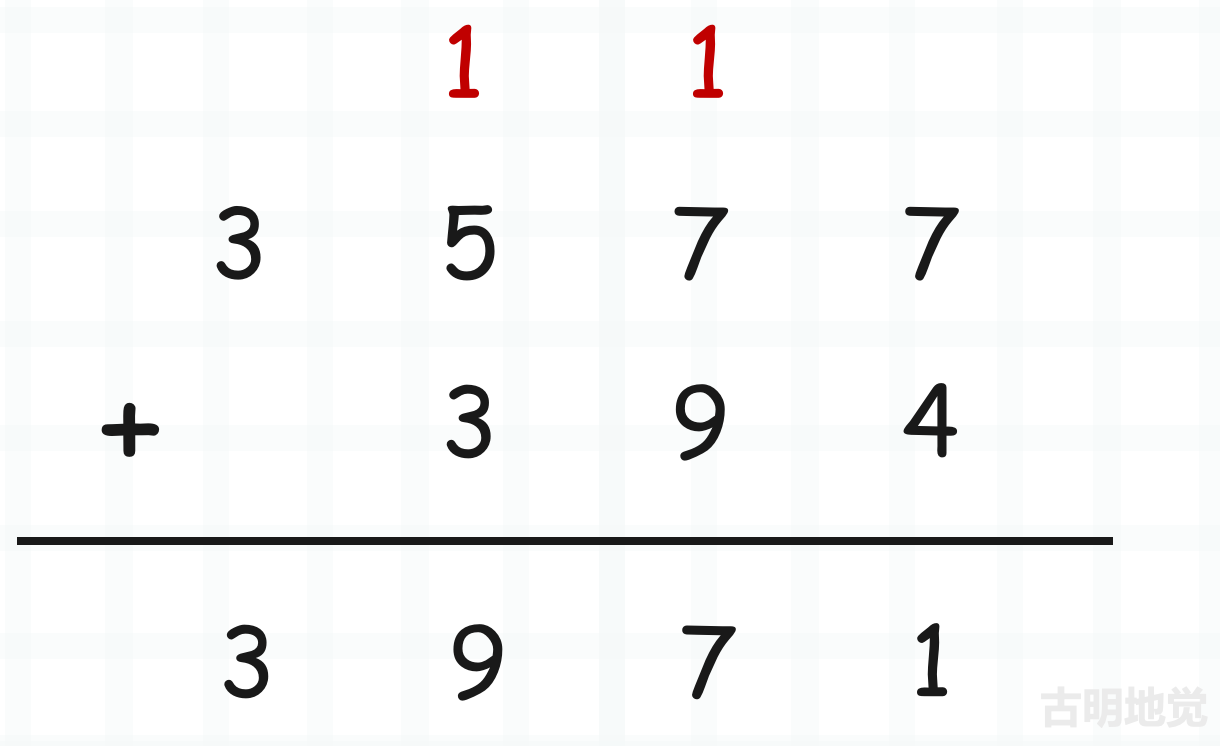
从最低位开始进行相加,逢十进一,ob_digit 也是同理。我们可以把数组中的每一个元素看成是一个整体,只不过它不再是逢十进一,而是逢 2 ** 30 进一。
# 数组的每个元素最大能表示 2 ** 30 - 1
# 把元素整体想象成我们生活中加法的个位、十位、百位...
# 然后对应的位相加,逢 2 ** 30 进一
a = [1024, 22]
b = [342, 18]
c = [1024 + 342, 22 + 18] # [1366, 40]
print(
a[0] + a[1] * 2 ** 30
+
b[0] + b[1] * 2 ** 30
==
c[0] + c[1] * 2 ** 30
) # True
所以仍旧是对应的位进行相加,和我们生活中的加法并无本质上的区别。只不过生活中的加法,每一位能表示 0~9,逢十进一。而 Python 底层的加法,因为整数使用数组存储,那么每一个位能表示 0 ~ 2 ** 30 - 1,逢 2 ** 30 进一。
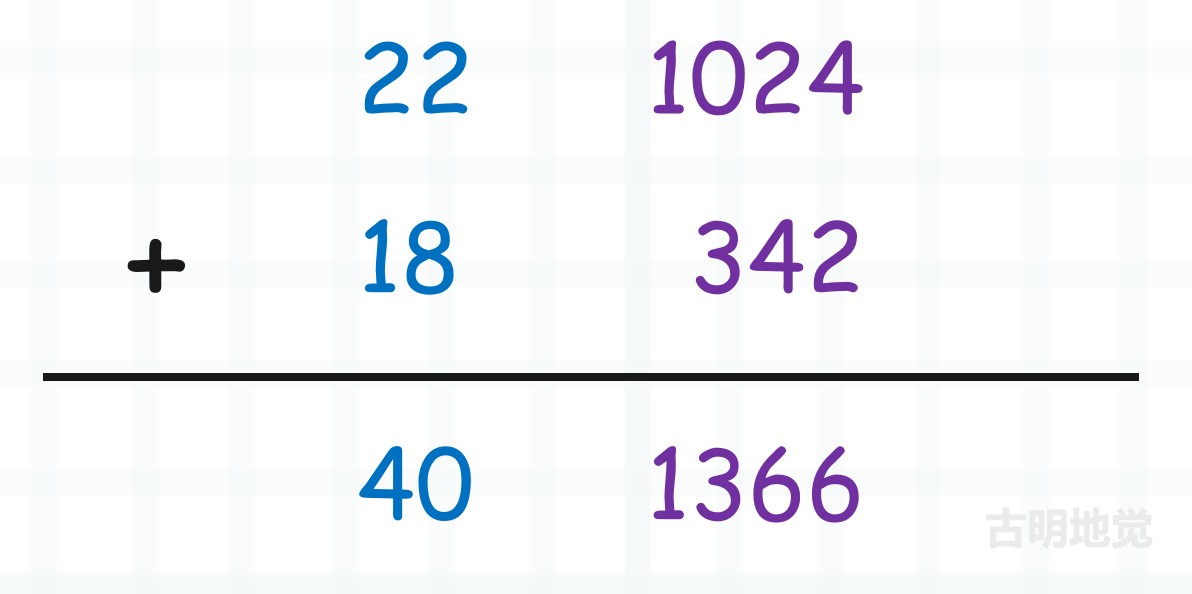
把 1024、342 想象成个位,把 22、18 想象成十位,并且此时不再是逢十进一,而是逢 2 ** 30 进一。
a = [2 ** 30 - 1, 16]
b = [2 ** 30 - 1, 21]
# a[0] + b[0] 超过了 2 ** 30,要进个 1
# 而逢十进一之后,该位要减去十
# 那么逢 2 ** 30 进一之后,显然要减去 2 ** 30
c = [
a[0] + b[0] - 2 ** 30,
a[1] + b[1] + 1
]
print(
a[0] + a[1] * 2 ** 30
+
b[0] + b[1] * 2 ** 30
==
c[0] + c[1] * 2 ** 30
) # True
然后是绝对值减法,和绝对值加法一样,也可以类比生活中的减法,从低位到高位分别相减。如果某一位相减的时候发现不够了,那么要向高位借一位。比如 27 减去 9,由于 7 比 9 小,因此向 2 借一位变成 17,减去 9,得 8。但 2 被借了一位,所以剩下 1,因此结果为 18。
a = [5, 3]
b = [6, 1]
result = []
# 如果计算 a - b,整个过程是怎样的呢?
# 首先是 a[0] - b[0],由于 a[0] < b[0]
# 所以要借一位,而一个位是 2 ** 30
result.append(a[0] + 2 ** 30 - b[0])
# 然后是 a[1] - b[1]
# 由于 a[1] 被借走了一个位,因此要减 1
result.append(a[1] - 1 - b[1])
print(result) # [1073741823, 1]
# 验证一下
print(
(a[0] + a[1] * 2 ** 30)
-
(b[0] + b[1] * 2 ** 30)
) # 2147483647
print(
result[0] + result[1] * 2 ** 30
) # 2147483647
结果没有问题,以上我们就从原理上介绍了大整数的加减法,下面再看一下源码实现。
整数加减法源码实现
当整数相加时会执行 long_add 函数,看一下它的具体实现。
// Objects/longobject.c
static PyObject *
long_add(PyLongObject *a, PyLongObject *b)
{
PyLongObject *z; // 指向运算后的整数
CHECK_BINOP(a, b); // 确保 a 和 b 都指向整数
// 如果两个整数的 ob_digit 数组最多只有一个元素
// 那么取出来判断正负之后,直接进行运算即可
// 由于 2 ** 30 - 1 已经很大了,所以绝大部分场景,都会执行此分支
if (Py_ABS(Py_SIZE(a)) <= 1 && Py_ABS(Py_SIZE(b)) <= 1) {
// MEDIUM_VALUE 是一个宏,接收一个 abs(ob_size) <= 1 的 PyLongObject *
// 如果 ob_size 等于 0, 那么返回 0
// 如果 ob_size 等于 1, 那么返回 ob_digit[0]
// 如果 ob_size 等于 -1, 那么返回 -ob_digit[0]
// 所以计算出 MEDIUM_VALUE(a) + MEDIUM_VALUE(b) 之后
// 将结果转成 PyLongObject,然后返回其泛型指针即可
// 因此当数组中元素个数不超过 1 的时候,显然是可以直接相加的
return PyLong_FromLong(MEDIUM_VALUE(a) + MEDIUM_VALUE(b));
}
// 否则走通用分支
if (Py_SIZE(a) < 0) {
// 如果 a 是负数、b 是负数,那么先计算 |a| + |b|
if (Py_SIZE(b) < 0) {
z = x_add(a, b);
if (z != NULL) {
// 然后对 z 取相反数
assert(Py_REFCNT(z) == 1);
Py_SIZE(z) = -(Py_SIZE(z));
}
}
// 如果 a 是负数、b 是正数,那么计算 |b| - |a|
else
z = x_sub(b, a);
}
else {
// 如果 a 是正数、b 是负数,那么计算 |a| - |b|
if (Py_SIZE(b) < 0)
z = x_sub(a, b);
// 如果 a 是正数、b 是正数,那么计算 |a| + |b|
else
z = x_add(a, b);
}
return (PyObject *)z;
}
因此 long_add 函数并不长,但是调用了 x_add 和 x_sub,显然核心逻辑是在这两个函数里面。至于 long_add 函数,它的逻辑如下:
- 判断两个整数底层对应的数组的长度是否均小于等于 1,如果是的话那么通过宏 MEDIUM_VALUE 直接将其转成 C 的一个 digit,当然符号也会考虑在内。然后直接相加、返回即可。显然这里走的是快分支,或者说快速通道。
- 但如果其中一方的数组长度(ob_size)大于 1,那么判断两者的符号。如果都为负数,那么通过 x_add 计算两者的绝对值之和,然后取相反数。
- 如果 a 为负数,b 为正数,那么通过 x_sub 计算 b 和 a 的绝对值之差即可;
- 如果 a 为正数,b 为负数,那么通过 x_sub 计算 a 和 b 的绝对值之差即可;
- 如果都为正数,那么通过 x_add 计算 a 和 b 的绝对值之和即可;
所以 Python 整数设计的非常巧妙,ob_digit 虽然用来维护具体数值,但它并没有考虑正负,整数的正负是通过 ob_size 来表示的。通过将运算变成绝对值运算,实现起来会方便很多。
说完了 long_add,再来看看 long_sub,这两者是类似的。
// Objects/longobject.c
static PyObject *
long_sub(PyLongObject *a, PyLongObject *b)
{
PyLongObject *z; // 指向运算后的整数
CHECK_BINOP(a, b); // 确保 a 和 b 都指向整数
// 如果两个整数的 ob_digit 数组最多只有一个元素
// 那么取出来判断正负之后,直接进行运算即可
if (Py_ABS(Py_SIZE(a)) <= 1 && Py_ABS(Py_SIZE(b)) <= 1) {
return PyLong_FromLong(MEDIUM_VALUE(a) - MEDIUM_VALUE(b));
}
// 否则走通用分支
if (Py_SIZE(a) < 0) {
// 如果 a 是负数、b 是负数,那么先计算 |a| - |b|
if (Py_SIZE(b) < 0)
z = x_sub(a, b);
// 如果 a 是负数、b 是正数,那么先计算 |a| + |b|
else
z = x_add(a, b);
// 然后对 z 取相反数
if (z != NULL) {
assert(Py_SIZE(z) == 0 || Py_REFCNT(z) == 1);
Py_SIZE(z) = -(Py_SIZE(z));
}
}
else {
// 如果 a 是正数、b 是负数,那么计算 |a| + |b|
if (Py_SIZE(b) < 0)
z = x_add(a, b);
// 如果 a 是正数、b 是正数,那么计算 |a| - |b|
else
z = x_sub(a, b);
}
return (PyObject *)z;
}
所以 long_add 和 long_sub 的代码是类似的,它们将整数的运算转成了整数的绝对值运算,所以关键要理解什么时候用 x_add,什么时候用 x_sub。
a + b
- 如果 a 是正数,b 是正数,调用 x_add(a, b),计算 |a| + |b|;
- 如果 a 是负数、b 是负数,调用 x_add(a, b),计算 |a| + |b|,然后再取反;
- 如果 a 是正数、b 是负数,调用 x_sub(a, b),计算 |a| - |b|;
- 如果 a 是负数、b 是正数,调用 x_sub(b, a),计算 |b| - |a|;
所以相加时,符号相同会调用 x_add、符号不同会调用 x_sub。
a - b
- 如果 a 是正数、b 是负数,调用 x_add(a, b),计算 |a| + |b|;
- 如果 a 是负数、b 是正数,调用 x_add(a, b),计算 |a| + |b|,然后再取反;
- 如果 a 是正数,b 是正数,调用 x_sub(a, b),计算 |a| - |b|;
- 如果 a 是负数,b 是负数,调用 x_sub(b, a),计算 |b| - |a|。当然在源码中调用的是 x_sub(a, b),计算 |a| - |b|,然后再取相反数;
所以相减时,符号相同会调用 x_sub、符号不同会调用 x_add。
接下来我们的重点就是绝对值加法和绝对值减法的具体实现细节。
绝对值加法:x_add
函数 x_add 负责绝对值加法,但是介绍之前,需要先了解几个宏,它们在 x_add 中会有体现。
// Include/longintrepr.h
#define PyLong_SHIFT 30
#define PyLong_BASE ((digit)1 << PyLong_SHIFT)
#define PyLong_MASK ((digit)(PyLong_BASE - 1))
显然 PyLong_BASE 等于 2 ** 30,PyLong_MASK 等于 2 ** 30 - 1(说明 32 个位,前两个位是 0,后三十个位都是 1)。
然后我们可以看 x_add 的具体实现了。
// Objects/longobject.c
static PyLongObject *
x_add(PyLongObject *a, PyLongObject *b)
{
// 参数 a 和 b 指向了两个要相加的整数对象
// 获取整数在底层的 ob_size
Py_ssize_t size_a = Py_ABS(Py_SIZE(a)), size_b = Py_ABS(Py_SIZE(b));
// 指向两个整数的相加结果
PyLongObject *z;
// 循环变量
Py_ssize_t i;
// 每个部分的运算结果
digit carry = 0;
// 如果 size_a 小于 size_b,说明 |a| < |b|
// 那么将两个整数交换位置,确保操作符左边的数大于右边的数
// 这么做也符合人类习惯,可以想象一下小学时候的加法计算
// 如果一个位数多,一个位数少,也会习惯将位数多的放在左边
if (size_a < size_b) {
{ PyLongObject *temp = a; a = b; b = temp; }
{ Py_ssize_t size_temp = size_a;
size_a = size_b;
size_b = size_temp; }
}
// 申请一个 ob_digit 的长度为 size_a + 1 的 PyLongObject
// 但为什么是 size_a + 1 呢? 由于上面的 if 语句,使得 size_a 一定不小于 size_b
// 那么 a 和 b 相加之后的 z 的 ob_size 一定不小于 size_a
// 但是也可能比 size_a 多 1,比如: a = 2 ** 60 - 1, b = 1
// 那么相加之后结果为 2 ** 60,于是 ob_size 就变成了 3
// 因此在创建 z 的时候,ob_digit 的容量会等于 size_a + 1
z = _PyLong_New(size_a+1);
// 正常情况下, z 是一个 PyLongObject *,但如果 z == NULL, 表示分配失败(程序崩溃)
// 但说实话, 除非你内存不够了, 否则这种情况不会发生
if (z == NULL)
return NULL;
// 重点来了,因为 size_a > size_b,所以会以 size_b 为准,两者从低位向高位依次对应相加
// 当 b 到头了,再单独算 a 的剩余部分
// 因此以 i < size_b 作为条件
for (i = 0; i < size_b; ++i) {
// 将 a->ob_digit[i] + b->ob_digit[i] + carry(初始为 0)作为 carry
// 如果 carry 没有超过 2 ** 30 - 1,那么它就是 z -> ob_digit[i] 的值
carry += a->ob_digit[i] + b->ob_digit[i];
// 但 carry 是可能溢出的,当溢出时,应该要减去 2 ** 30,所以还要判断是否产生了进位
// 但解释器没有使用常规的判断,而是选择了效率更高的位运算(carry & PyLong_MASK)
// 由于 PyLong_MASK 等于 (1 << 30) - 1,所以它的前两个位是 0,后面三十个位全是 1
// 因此当 carry 不超过 2 ** 30 - 1 时,carry & PyLong_MASK 就等于 carry
// 当 carry 超过 2 ** 30 - 1 时,carry & PyLong_MASK 就等于 carry - 2 ** 30
z->ob_digit[i] = carry & PyLong_MASK;
// 然后当 carry 产生进位时,显然不可以丢,它们要作用在数组中下一个元素相加的结果上
// 所以这里将 carry 右移 30 位,得到进位,然后重新赋值给 carry,并作用在下一轮循环中
// 如果没有产生进位,那么 carry 为 0,如果产生了进位,那么 carry 为 1
carry >>= PyLong_SHIFT;
}
// 如果 b 到头了, 那么继续从当前的 i 开始遍历,直到 i == size_a, 逻辑还是和上面一样
for (; i < size_a; ++i) {
// 此时只需要加上 a->ob_digit[i] 和 carry 即可,因为 b 到头了
carry += a->ob_digit[i];
// 这里也要按位与 PyLong_MASK, 因为也可能存在进位的情况
// 拿生活中的 99999 + 1 为例,此时 a = 99999, b = 1,显然第一次循环 b 就到头了
// 但后面单独循环 a 的时候, 依旧会产生进位,所以这里也是同理
z->ob_digit[i] = carry & PyLong_MASK;
// carry 右移 30 位得到进位,然后重新赋值给 carry
carry >>= PyLong_SHIFT;
}
// 两个循环结束之后, 其实还差一步,还拿 99999 + 1 举例子
// 按照顺序相加得到的是 00000,因为最后还进了一个 1,这里的 carry 也是同理
// 因此 z 的 ob_size 要比 size_a 多 1,目的就在于此
// 所以要将 z->ob_digit 的最后一个元素设置成 carry
z->ob_digit[i] = carry;
// 但如果最后的 carry 没有进位的话,显然其结果就是 0
// 所以最后没有直接返回 z,而是返回了 long_normalize(z)
// 这个 long_normalize 函数的作用是从后往前依次检查 ob_digit 的元素
// 如果为 0,那么就将其 ob_size 减去 1, 直到出现一个不为 0 的元素
// 比如 ob_digit 为 [0, 3, 1, 0, 0, 0],长度为 6,但规范化之后的 ob_size 显然是 3
// 不过对于当前来说,显然最多只会检查一次,因为它的 ob_size 只比 size_a 多 1
// 所以判断数组最后一个元素是否为 0 也可以,如果为 0 则说明没有产生进位
return long_normalize(z);
}
整数在底层实现的很巧妙,不理解的话可以多看几遍,然后我们在 Python 的层面上再反推一下绝对值加法,进一步感受底层的运算过程。
# 假设有 a 和 b 两个整数
# 当然这里是使用列表直接模拟底层数组 ob_digit
a = [1073741744, 999, 765, 123341]
b = [841, 1073741633, 2332]
# 然后创建 z,表示 a 和 b 的相加结果
z = []
# 为了更直观,我们一步步手动相加
# 首先是 a[0] + b[0],得到 carry
carry = a[0] + b[0]
# 但 carry 可能大于 2 ** 30 - 1,所以要进行判断
# 如果大于,那么要减去 2 ** 30,否则保持不变
# 而这一步可以使用位运算来实现,将 carry 和 (2 ** 30 - 1) 按位与即可
print(carry & (2 ** 30 - 1)) # 761
# 结果是 761,说明 carry 比 2 ** 30 - 1 大
# 然后 z 的第一个元素就是 761
z.append(761)
# 接着计算 a[1] + b[1] 得到新的 carry
# 但是之前的 carry 大于 2 ** 30 - 1,所以还要再加上 carry >> 30,即进位
# 当然,如果没有产生进位,那么 carry >> 30 就是 0
carry = (carry >> 30) + a[1] + b[1]
# 然后 carry & (2 ** 30 - 1) 得到 809,说明 carry 依旧大于 2 ** 30 - 1
print(carry & (2 ** 30 - 1)) # 809
# 所以 z 的第二个元素就是 809
z.append(809)
# 计算 a[2] + b[2] 的时候也是同理
carry = (carry >> 30) + a[2] + b[2]
# 但显然此时的 carry 已经不大于 2 ** 30 - 1 了
print(carry & (2 ** 30 - 1)) # 3098
# 说明 z 的第三个元素是 3098
z.append(3098)
# 此时 b 到头了,所以直接将 a[3] 作为 carry
# 当然还要判断上一步的 carry 是否大于 2 ** 30 - 1
# 所以还是右移 30 位,当不大于 2 ** 30 - 1 时,carry >> 30 就是 0
carry = (carry >> 30) + a[3]
print(carry & (2 ** 30 - 1)) # 123341
z.append(123341)
# 此时 a 也遍历完毕,但是不要忘记再对 carry 进行判断
# 如果大于 2 ** 30 - 1,那么会产生进位,所以 z 还要再 append 一个 1
# 当然这里 carry 没有超过 2 ** 30 - 1
# 此时 z 为 [761, 809, 3098, 123341]
print(z) # [761, 809, 3098, 123341]
# a = [1073741744, 999, 765, 123341]
# b = [841, 1073741633, 2332]
# z = [761, 809, 3098, 123341]
# 因此 ob_digit 为 [1073741744, 999, 765, 123341]
# 和 ob_digit 为 [841, 1073741633, 2332] 的两个 PyLongObject 相加
# 得到的新的 PyLongObject 的 ob_digit 为 [761, 809, 3098, 123341]
print(
a[0] + a[1] * 2 ** 30 + a[2] * 2 ** 60 + a[3] * 2 ** 90
+
b[0] + b[1] * 2 ** 30 + b[2] * 2 ** 60
==
z[0] + z[1] * 2 ** 30 + z[2] * 2 ** 60 + z[3] * 2 ** 90
) # True
以上就是绝对值加法,我们从源码的角度和 Python 代码的角度分别解释了一遍。看完了绝对值加法,再来看看绝对值减法。
绝对值减法:x_sub
和绝对值加法一样,绝对值减法也可以类比生活中的减法,从低位到高位分别相减。如果某一位相减的时候发现不够了,那么要向高位借一位。比如 27 减去 9,7 比 9 小,因此向 2 借一位变成 17,减去 9,得 8。但 2 被借了一位,所以剩下 1,因此结果为 17。
// Objects/longobject.c
static PyLongObject *
x_sub(PyLongObject *a, PyLongObject *b)
{
// 依旧是获取两者的 ob_size 的绝对值
Py_ssize_t size_a = Py_ABS(Py_SIZE(a)), size_b = Py_ABS(Py_SIZE(b));
// z 指向相加之后的 PyLongObject
PyLongObject *z;
// 循环变量
Py_ssize_t i;
// 如果 size_a 小于 size_b,那么 sign 就是 -1,否则就是 1
int sign = 1;
// 之前 carry 保存相加的结果,这里的 borrow 保存相减的结果
// 名字很形象,相加要进位叫 carry,相减要借位叫 borrow
digit borrow = 0;
// 接下来依旧要判断两个整数的大小,确保相减的时候,绝对值大的一方在左边
// 相加的时候,大的一方在左边还是在右边,其实没太大影响
// 而相减的时候如果大的一方在左边,显然会省事很多
// 所以如果 size_a 比 size_b 小,说明 a 的绝对值比 b 小
if (size_a < size_b) {
// 那么令 sign = -1,因为 a 和 b 交换了位置,所以后续相减之后还要再乘上 sign
// 因为计算的是绝对值之差,符号是在绝对值之差计算完毕之后通过 sign 判断的
sign = -1;
// 交换 a 和 b 的位置
{ PyLongObject *temp = a; a = b; b = temp; }
{ Py_ssize_t size_temp = size_a;
size_a = size_b;
size_b = size_temp; }
}
// 如果 size_a == size_b,那么需要依次比较 ob_digit 里的元素,才能判断出大小
else if (size_a == size_b) {
// 所以从 ob_digit 的尾部开始遍历
i = size_a;
while (--i >= 0 && a->ob_digit[i] == b->ob_digit[i])
;
// 如果所有元素都相等,那么 i 会等于 -1,相减的结果为 0,此时直接返回 0 即可
// 所以这一步也是为了能够快速返回结果,而额外做的一层判断
if (i < 0)
return (PyLongObject *)PyLong_FromLong(0);
// 但如果某个对应的元素不相等,那么只需判断这两者谁大谁小即可
// 假设 a 的 ob_digit 是 [2, 3, 4, 5],b 的 ob_digit 是 [1, 2, 4, 5]
// 那么上面的 while 循环结束之后,i 会等于 1,显然只需要判断索引为 1 时,对应的值谁大谁小即可
if (a->ob_digit[i] < b->ob_digit[i]) {
// 如果 a->ob_digit[i] < b->ob_digit[i],同样说明 a 小于 b
// 那么将 sign 设置为 -1,并交换 a 和 b 的位置
sign = -1;
{ PyLongObject *temp = a; a = b; b = temp; }
}
// 因为高位在减法的时候会被抵消掉,所以将 size_a 和 size_b 设置成 i + 1 即可
// 假设两个整数的 ob_digit 分别是 [2, 3, 4, 5] 和 [1, 2, 4, 5]
// 因为后两个元素是一样的,所以后续只需要对索引为 [0: i+1] 的部分做差即可
size_a = size_b = i+1;
}
// a 和 b 相减之后,结果一定不超过 a,因此 ob_digit 的长度一定小于等于 size_a
z = _PyLong_New(size_a);
if (z == NULL)
return NULL;
// 然后下面的逻辑和 x_add 是类似的
for (i = 0; i < size_b; ++i) {
// 让 a 的 ob_digit[i] 减去 b 的 ob_digit[i]
// 当然,由于上一个元素在相减的时候,可能会向当前元素借位,因此还要再减去 borrow
// 如果没借位,那么 borrow 是 0,如果借位了,那么 borrow 是 1
// 然后如果当前元素相减的结果也小于 0,那么继续向下一个元素借位
// 但我们似乎没有看到借位的逻辑,这是因为 digit 是无符号 32 位整型,负数会发生环绕
// 假设这里相减得到的是 -100,那么结果就是 2 ** 32 - 100
// 所以存储的负数会变成 "2 ** 32 + 该负数",相当于自动向数组的下一个元素借了一位
// 但 digit 只用 30 个位,所以借一位之后应该加上 2 ** 30,而目前加的是 2 ** 32
borrow = a->ob_digit[i] - b->ob_digit[i] - borrow;
// 所以还要和 PyLong_MASK 按位与,只保留后 30 个位的值
// 当然如果没有产生借位,borrow & PyLong_MASK 的结果还是 borrow
z->ob_digit[i] = borrow & PyLong_MASK;
// 如果借位了,下一轮循环的时候,肯定要多减个 1,但问题是怎么判断有没有借位呢?
// 很简单,如果没有借位,borrow 一定小于 2 ** 30,第 31 个位一定是 0
// 如果借位了,那么 borrow 一定大于 2 ** 30,第 31 个位一定是 1
// 所以让 borrow 右移 30 个位
borrow >>= PyLong_SHIFT;
// 然后和 1 按位与,如果产生了借位,borrow 就是 1,否则就是 0
// 等到下一轮循环的时候,再减去 borrow
borrow &= 1;
/*
所以 Python 底层的整数只用 30 个位真的非常巧妙,尤其是在减法的时候
由于 digit 是 32 位,借位时会加上 2 ** 32
但底层只用 30 个位,所以再和 PyLong_MASK 按位与,只保留后 30 个位
而当前元素如果借位了,那么数组下一个元素要减去 1,但怎么判断它有没有借位呢?
首先两个不超过 2 ** 30 - 1 的数,相减的结果如果为正(没产生借位)
那么一定也不会超过 2 ** 30 - 1,换句话说其结果对应的第 31 位一定是 0
但如果两个整数相减的结果为负,那么会自动加上 2 ** 32,因此第 31 位一定是 1
所以再让 borrow 右移 30 位,并和 1 按位与
如果结果为 1,证明相减为负数,确实向下一个元素借了 1,因此下一次循环时会多减一个 1
如果结果为 0,那么说明没有借位,下一次循环时相当于多减了一个 0
*/
}
// 如果 size_a 和 size_b 不相等,那么还需要继续处理 a 的 ob_digit 剩余的元素
for (; i < size_a; ++i) {
// 这里的逻辑和之前分析 x_add 是类似的
borrow = a->ob_digit[i] - borrow;
z->ob_digit[i] = borrow & PyLong_MASK;
borrow >>= PyLong_SHIFT;
borrow &= 1;
} // 只不过由于不会产生进位,因此不需要再对 borrow 做额外判断
// 而 x_add 中最后还要判断 carry 有没有进位
assert(borrow == 0);
// 如果 sign < 0,那么证明是负数,因此还要改变 z 的符号
if (sign < 0) {
Py_SIZE(z) = -Py_SIZE(z);
}
// 最后同样要将 z 规范化,将高位的 0 忽略掉
// 比如 100000 - 99999,结果是 000001,显然只需要保留最低位的 1 即可
// 另外如果相减的结果是小整数,那么直接从池子里获取,否则返回新创建的
return long_normalize(z);
}
同样的,关于绝对值减法,我们也用 Python 代码演示一遍,感受底层的运算过程。
a = [5, 3]
b = [6, 1]
result = []
# 如果计算 a - b,整个过程是怎样的呢?
# 首先是 a[0] - b[0],由于 a[0] < b[0],所以要借一位,而一个位是 2 ** 30
result.append(a[0] + 2 ** 30 - b[0])
# 注:源码中加的是 2 ** 32,所以之后还要和 PyLong_MASK 按位与
# 因此 a[0] + 2 ** 30 - b[0] 等价于 (a[0] + 2 ** 32 - b[0]) & (2 ** 30 - 1)
# 然后是 a[1] - b[1],由于 a[1] 被借走了一个位,因此要减 1
result.append(a[1] - 1 - b[1])
print(result) # [1073741823, 1]
# 验证一下
print(
(a[0] + a[1] * 2 ** 30)
-
(b[0] + b[1] * 2 ** 30)
) # 2147483647
print(
result[0] + result[1] * 2 ** 30
) # 2147483647
以上就是绝对值减法,设计的非常巧妙,可以多看几遍,并用列表模拟 ob_digit 数组,然后实际测试一下。
小结
关于整数的内容,我们就介绍完了。回顾一下,首先我们剖析了整数的底层实现,了解了它不会溢出的奥秘,然后又介绍了小整数对象池。但也正如之前所说,使用数组实现大整数并不是什么特别新颖的思路,它的难点在于数学运算,这是非常考验编程技巧的地方。
而我们这里只是分析了加减法,至于乘除则更加复杂,这里就不再分析了。关于乘法,解释器采用的是效率更高的 karatsuba 算法,比较有意思,有兴趣可以自己查看一下。
综上所述不难发现 Python 效率低的原因,毕竟一个简单的整数运算都要做这么多工作。当然了,解释器内部也定义了很多快分支,会提前检测能否使用快速通道进行处理,当无法使用快速通道时,再走通用逻辑。
欢迎大家关注我的公众号:古明地觉的编程教室。

如果觉得文章对你有所帮助,也可以请作者吃个馒头,Thanks♪(・ω・)ノ。